严格意义上讲,这篇文章应该算一篇读书笔记,书名为《编码:隐匿在计算机软硬件背后的语言》,相信很多人都听过这本书,但和很多经典技术书籍一样,很多人对这本书依旧只停留在听说这个层面(算法导论可能算个例外),所以在此,我再次向所有学软/硬件的童鞋推荐这本书,尤其是没有过多精力研究硬件的软件工程师们,这本书绝对会让你对计算机的底层硬件有一个突破性的认识。
回到正题,在开始做计数器之前,有必要介绍下数字电路和门电路,wiki上关于数字电路的定义为『由门电路构成的复杂电路』,所以这么看来重点就在门电路上面了,但如果从门电路的核心晶体管讲起,那就是在写书而非博客了,所以关于门电路的部分请各位直接参照wiki上的描述即可——我想任何有点逻辑基础的童鞋相信都是能看懂的,如果依旧无法理解,请翻看任意一本讲离散数学或门电路的书籍后再回来阅读此文。
数字电路分为组合逻辑电路和时序逻辑电路,它们的不同点在于组合逻辑电路的输出仅由输入决定,而时序逻辑电路的输出由输入和电路状态共同决定,前者很好理解,以『与门』为例子,任何一对输入显然只产生一种输出结果,那和电路状态的关联是如何产生的呢?
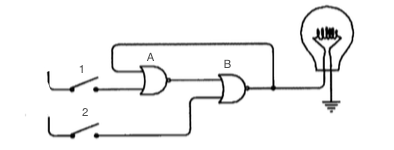
让我们先来分析上面这张图,灯初始为熄灭的,闭合开关1,A下端输入口为1(以1-0表示高低电频方便叙述),B下端输入口为0,灯是熄灭的,则B的输出口和A的上输入口均为0,因此A的输出口为0(0 或非 1 == 0),但B的输出口又变为1(0 或非 0 == 1),此时灯亮,A输出状态开始反向,接着B输出状态也开始反向——即回到初始状态,然后进行上述循环——即得到一个不断闪烁的灯。
接着让我们闭合开关1,进行类似上面的分析,你会发现灯泡依旧呈闪烁状态。额,惊讶么?同样是两个开关断开(即输入均为0),得到的结果却是一个是熄灭的(即输出为0),另一个是闪烁的(1-0变换),回头看前面所说的时序电路的和状态有关,这不就是活生生的例子么!其实类似的例子很多,而所有类似在断开下有两个稳态的电路都称为触发器,下图就是上面电路的元器件版本——最简单的R-S(复位-置位)触发器
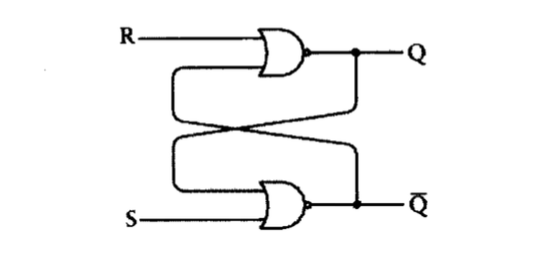
R-S触发器的特点是能记住哪个输入端最终状态为1,但是要想记住某个特定时间点上信号是0或1,那R-S触发器就无能为力了,现在通过修改R-S触发器来得到我们想要的功能,直接上图
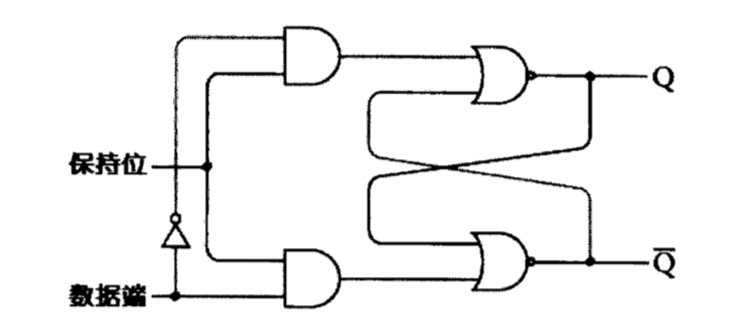
这个电路称为电平触发的D型触发器,不过习惯上D型触发器把保持位叫做时钟。如果把数据端简写为D,时钟端简写为Clk,则其功能表如下
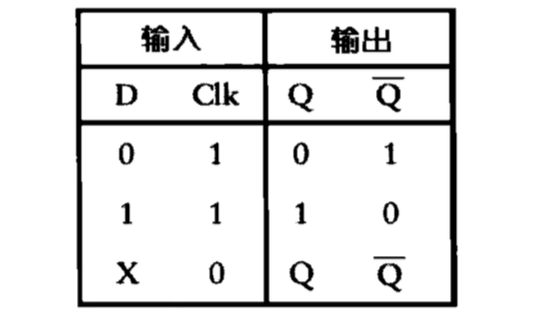
这时候,如果我们想做一个抢答器,用电平触发的D型触发器就绰绰有余了,但如果我们想做个计数器,电平触发的方法就显得有点力不从心了,因为计数器的各个二进制计数位增减的频率不同,电平触发很难协调好这种不同,但仔细观察就会发现任意位二进制计数位变化的频率刚好是后一位的两倍,所以如果可以设计出让前一位变化第二次的瞬间引起下一位变化的电路,那计数器的问题就迎刃而解了。当然,这个问题已经解决,用到的就是边沿触发的D型触发器,图示如下
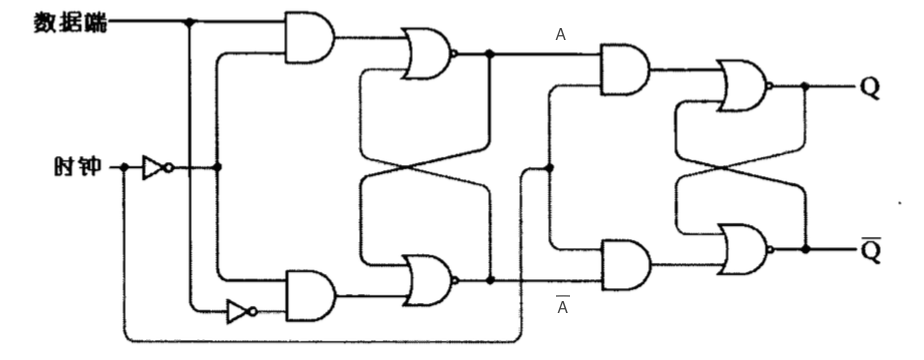
其简图如下
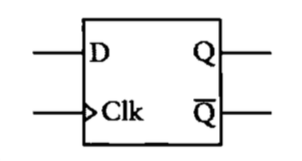
为什么称这个电路为边沿触发的呢?让我们仔细观察上面这个图,你会发现它其实是由两个电平触发的D型触发器拼接起来的,左边的触发器由一个数据端提供相反的两个输入位,右边的触发器则由左边触发器的输出端提供——显然正好是两个相反的输入位;而两个触发器的时钟则共用一个时钟输入口,但取值正好相反。
现在,结合前面电平触发的D型触发器的功能表来看,若初始状态下数据端和时钟均为0,根据功能表A为1,Q保持状态不变,突然改变时钟为1,A的状态保持不变,右边的触发器就变为1/1/0的输入,Q如果原来为0则仍然为0,如果原来为1则变为0;若初始状态下数据端为1时钟为0,根据功能表A为0,Q保持状态不变,突然改变时钟为1,A的状态保持不变,右边的触发器变为0/1/1的输入,Q如果原来为1则仍然为1,如果原来为0则变为1;至于其它任何变化态下的时钟为0,输出均保持不变。
根据上面的分析,发现只有当时钟由0变为1(电气中称为『正跳变』)才能引起输出的变化,但是有个问题,在Q的初始状态和数据端相反的时候,正跳变也不会引起输出的变化,怎样保证正跳变一定引起输出的变化呢?将非Q和数据端连接就可以了。
说到这里,边沿触发的D型触发器说完了,但怎样应用呢?前面说了,计数器要保证前一位变化两次才引起后一位的变化,那边沿触发的D型触发器刚好满足需求,因为时钟的每次周期变换都改变了两次,但只有一次是正跳变(显然另一次就是负跳变),所以理论就是时钟引起第一位变,第一位引起第二位变。。。
那时钟应该怎样设计呢?最简单的显然就是一个闭合的非门电路,非门电路的输出口用于输出(实际同时也相当于输入)。到此,时钟和计数器的设计完成,拼接出来的结果如下
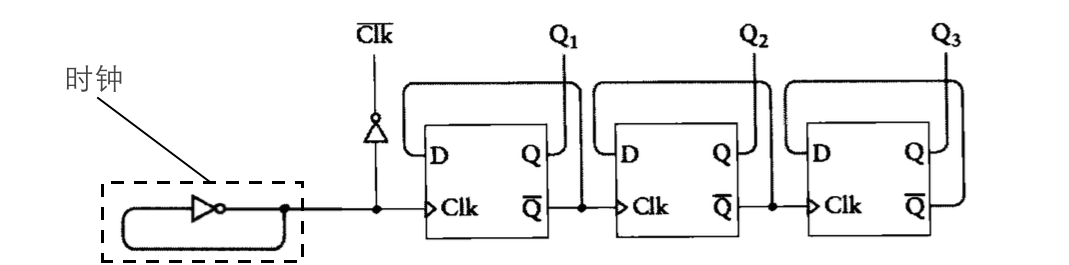
为了证明这个计数器是对的,我们还是分析一下输出,得到的结果如下
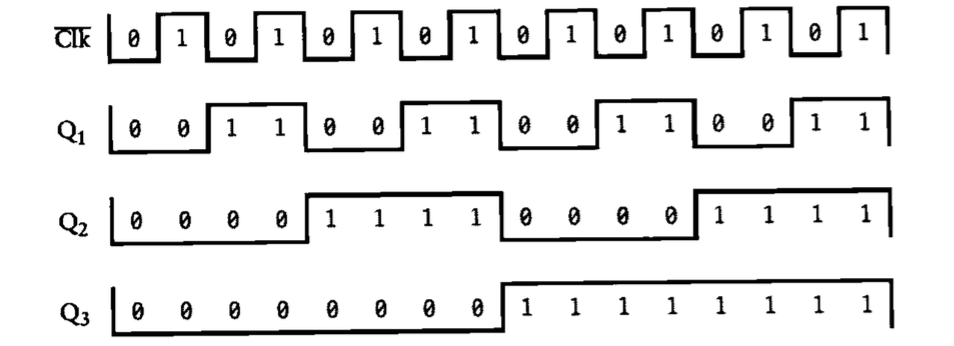
观察Q3Q2Q1组成的3位二进制,很眼熟对吧,它们就是按时钟每个频率变化的二进制数,从0-7,而这也就证明了我们计数器的理论正确性。
回头看这篇文章,似乎一个计数器并不复杂,但若要你在掌握门电路的基础上凭空设计电路,你就会发现举步维艰,而这也是逻辑电路设计的魅力。
彩蛋:为什么主频越高电脑越快
这个问题貌似有点无厘头了,但回顾上面的内容就会发现,这并非显而易见的,而是切切实实可以通过理论来解释的:以计数器为例子,每次计数都是一个时钟周期,那时钟周期越短,计数就越快,同理于计算机的运算,主频的提高并不能减少迈的步子数,但却能大大缩短每次『迈步』的时间,也由此减少了相同指令的执行时间,所以『主频越高电脑越快』结论成立。