AImager

去年在Matrix大牛的博客上看到了一篇关于自我指涉的文章，十分有趣，当时就尝试了下，并且在了解原理后随即构造了一些公式和图形，由于当时并没有时间管理博客，所以仅仅是记了一些相关的笔记，今天偶然发现文件夹中还有这些有趣的东西，就拿出来和大家分享下。

来看看下面这个数：
N=960939379918958884971672962127852754715004339660129306651505519271702802395266424689642842174350718121267153782770623355993237280874144307891325963941337723487857735749823926629715517173716995165232890538221612403238855866184013235585136048828693337902491454229288667081096184496091705183454067827731551705405381627380967602565625016981482083418783163849115590225610003652351370343874461848378737238198224849863465033159410054974700593138339226497249461751545728366702369745461014655997933798537483143786841806593422227898388722980000748404719

看到这个数，你的第一反应也许就是这个数很大，但除此之外，你应该难以想到任何和这个数有关的东西了，那么这个数到底有什么玄妙呢？别急，让我们先来画出下面这个公式在选定范围的二维图像：

我最后用Mathematica实现的图形效果如下（由于我对Mathematica的数值精度问题不是很了解，超大数时总是报错，所以改用矩阵形式实现）：

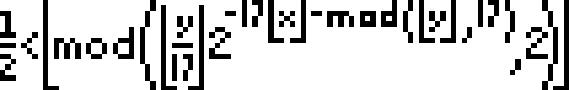
仔细看这个图，你发现了什么？是的，它和其对应的公式完全一样，这是多么神奇的事——一个公式的图像中居然含有其公式本身！！！那么这究竟是什么原因呢？下面就让我们仔细分析下：

首先看中间的 $\left \lfloor \frac{y}{17} \right \rfloor 2^{-17\left \lfloor x \right \rfloor - mod(\left \lfloor y \right \rfloor , 17)}$ 部分（暂且命名这个部分为Section），即类似于 $m*2^{k}$ 这种形式，了解二进制的人都会意识到，当 $k$ 为正数的时候，其结果就是将 $m$ 的二进制值左移 $k$ 位，而当 $k$ 小于0的时候，则是将 $m$ 的二进制值右移 $k$ 位，同时，如果 $m$ 的值不变， $k$ 的值顺序减小，那么得到的值将会是一串顺序右移的数；接着，公式又将Section对2取模，显然结果不是0就是1，而这个值刚好就是Section结果的最后一位；Ok，到此你应该理解了，其实公式右边就是不断得到 $\left \lfloor \frac{y}{17} \right \rfloor$ 中的二进制位，而且还是顺序的，不过它和图像由什么关系呢？其实这就是 $N$ 的意义了，你会发现 $\frac{N}{17}$ 刚好为整数，而得到的这个整数刚好是图像对应二进制数表示的十进制值（图像转换的二进制值是依据从左向右、从下向上的顺序得到的），所以 $\left \lfloor \frac{y}{17} \right \rfloor$ 的一串值刚好就是图像中的对应点（1表示黑色，0表示无），从而得到的就刚好是公式本身。

公式的核心原理懂了，那里面的17又是什么意思呢？仔细观察图片，17实际上就是可控图像的宽度，而对应 $N$ 的计算式为 $N = 17*图像的二进制表达式$ 。所以真实情况是 $N$ 的值是在图像确定后才算出来的。了解了公式的构造和 $N$ 值的确定，理论上我们就可以在某个公式图像的某个位置找出任何我们想要的图像，只要我们确定图像的范围（ $N$ 值）并同时确定公式就可以得到在指定公式下找到我们想要的图像。最后给出找出图像的通用公式（ $M$ 为区分小数部分的标识符， $L,H$ 为图像的长、高）

注：这里的公式只是为了方便图像找出的通用公式，并非找出图像的唯一公式

最后，附上自我指涉的Mathematica程序地址：mathematica-code